그래프, 그 첫 번째 이야기 | 인접행렬과 인접리스트

 정보과학, 그중에서도 '문제풀이(PS)'로 불리는 문제들에는 그래프가 정말로 많이 활용된다. 하지만 이 그래프는 우리가 흔히 생각하는

이런 그래프들은 아니다.

우리가 다룰 그래프들은

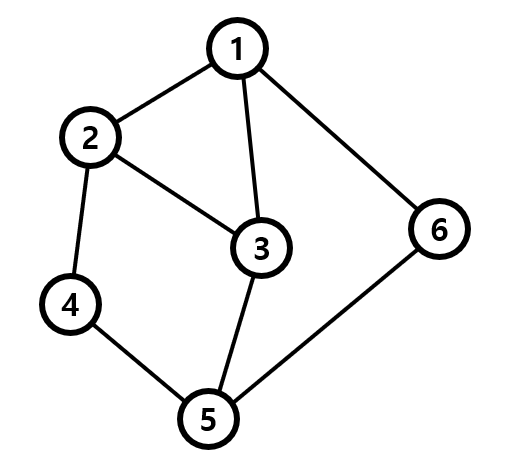
대충 이런 모양이다. 간단하게 정점간의 연결 관계라고 생각하면 편하다.

저 위 그림에서는 원이 정점, 정점 사이를 잇는 선이 간선이 된다.

정점은 영어로 node, vertex, point 등으로 쓰는데 셋의 차이는 거의 없다고 생각한다.

간선은 주로 edge라고 쓴다.

이를 코딩할 때 어떻게 쓰느냐.. 보통 인접행렬/ 인접 리스트로 많이 쓴다.

이 그래프를 인접행렬과 인접 리스트로 나타내 보자.

참고로 문제해결에서 거의 대부분의 그래프는 다음처럼 입력된다.

N : 정점 갯수

M : 간선 갯수

N M

$a_1$ $b_1$

$a_2$ $b_2$

......

$a_m$ $b_m$

이 때, $a_i$와 $b_i$ 사이에 간선이 존재하는 것이다.

인접행렬이란  정점간의 연결 관계를 행렬로 나타내는 것이다.

행렬의  i번째 행,j번째 열에 해당하는 위치에 1이 있으면 i와 j 사이에 간선이 있는 것이고, 0이 있으면 간선이 없는 것이다.

이를 시각화하면 다음과 같을 것이다.

인접행렬

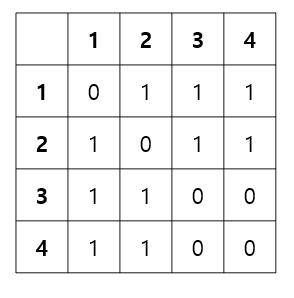
인접행렬은 구현하기도 쉽다. 이차원 배열에 숫자를 때려박기만 하면 된다.

#include <bits/stdc++.h>
using namespace std;
int graph[100][100];
int main()
{
	int n, m;
	int in1, in2;
	scanf("%d %d", &n, &m);
	for (int i = 0; i < m; i++)
	{
		scanf("%d %d", &in1, &in2);
		graph[in1][in2] = 1;
		graph[in2][in1] = 1;
	}
}

하지만 인접행렬은 난이도 높은 그래프 문제에서는 거의 쓰이지 않는다.

우선, 공간을 많이 잡아먹는다. 많은 그래프 문제에서 입력으로 주어지는 정점의 갯수는 만개에서 100만개 정도이다. 하지만 인접행렬은 정점 갯수의 제곱만큼 공간을 차지한다. 10000의 제곱만 해도 1억이니 메모리 초과가 난다.

또한, 두 정점을 잇는 간선이 여러개인 경우 표현이 곤란하다.

그래서 주로 문제해결에선 인접 리스트를 쓰게 될 것이다.

인접 리스트는 각 정점에 대해서 그 정점과 연결된 정점들을 모아 놓은 것이다. 

이를 시각화하면 다음과 같을 것이다.

인접 리스트

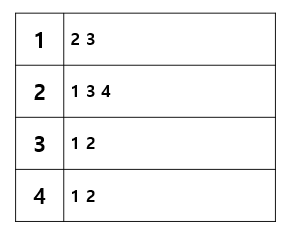
인접 리스트는 보통 vector 구조체를 통해 구현한다. 한 정점에 연결된 정점의 갯수(차수)가 제각각이기 때문이다.

#include <bits/stdc++.h>
using namespace std;
vector <int> graph[100];
int main()
{
	int n, m;
	int in1, in2;
	scanf("%d %d", &n, &m);
	for (int i = 0; i < m; i++)
	{
		scanf("%d %d", &in1, &in2);
		graph[in1].push_back(in2);
		graph[in2].push_back(in1);
	}
}

 

다음 번에는 그래프의 여러 종류에 대해 알아볼 것이다.